


 |
 |
 |
| Back to: | [Project Description] | [Student Work Homepage] | [Professional Stuff] |
Don Gossen & Kyle Prchal
06-04-97
Int. Math 2
Rules-
Over-Under is played with a full deck of cards with the two jokers removed. Over-Under can be played with any number of players, but five through ten players is most desirable. The minimum bet is five dollars and the maximum is 1000 dollars.
Objective-
The objective of Over-Under is to bet whether a card drawn will be under or over seven. If the gambler bets over seven and the card is over seven- any card from eight through king- the gambler wins. If the gambler bets under seven and the card drawn is under seven- any card from six through ace- the gambler wins. However, if the gambler bets over seven and the card drawn is seven or under the gambler loses. Also, if the gambler bets under seven and the card drawn is seven or over, the gambler loses. A seven card is an automatic loss for every gambler
How to Play-
All players (gamblers) place their bets prior to the dealer dealing a card. The dealer then draws a card and shows it to the player(s). The player(s) then sees if he/she won or lost. Then the dealer pays the winners and collects money from the losers. The card played is then inserted back into the deck and the cards are reshuffled. The player(s) then place their bets again.
Calculations-
The probability of a player winning is 24/52. This is found by using the equation:
number of favorable outcomes
number of possible outcomes.
The number of favorable outcomes is 24 because there are 24 cards either over seven or under seven from which to choose. These cards are:
| Under 7 | Over 7 |
| Ace, 2, 3, 4, 5, 6 in any suit | 8, 9, 10, Jack, Queen, King in any suit. |
The number of possible outcomes is 52 because there are 52 cards in a deck (without the jokers). The probability of winning, 24/52, never changes for each game because the cards are always put back in the deck so that there are always 52 cards and there are always 24 cards you can possibly pick to win.
Description of Simulation-
For the simulation we played Over-Under. The gambler (Kyle) called out either "over" or "under" and the amount of money he was betting. Then the dealer (Don) pulled a card from the top of the deck and showed to the gambler to see whether he had won or lost. We then recorded the results on a chart (see chart). The dealer then paid the gambler if he won or collected the money that the gambler bet if he lost. Then the dealer collected the card and shuffled it back into the deck. We repeated this 34 times and found that the casino/dealer win more ofter than the gambler(s).
Simulation Chart-
| Over/Under | Gambler Wins | Casino Wins |
|---|---|---|
| O | X | |
| O | X | |
| O | X | |
| O | X | |
| U | X | |
| O | X | |
| O | X | |
| O | X | |
| O | X | |
| O | X | |
| O | X | |
| U | X | |
| U | X | |
| O | X | |
| U | X | |
| U | X | |
| O | X | |
| U | X | |
| U | X | |
| O | X | |
| U | X | |
| U | X | |
| U | X | |
| O | X | |
| O | X | |
| U | X | |
| O | X | |
| U | X | |
| U | X | |
| O | X | |
| O | X | |
| U | X | |
| U | X | |
| U | X | |
| 14/34 | 20/34 |
O=Over U=Under
Collection-
The way this game is designed the casino will, statistically speaking, always win. To make this a fair game (in other words the casino and gambler have an equal probability of winning and losing) the following formula is used to determine the winning payoff:
number of possible outcomes x amount of bet
number of favorable outcomes
For example:
If a gambler bets five dollars he/she can find the amount that they will collect by multiplying five dollars and 52/24 (52/24 x 5). In other words, if the gambler collects $10.83 each time he wins making an initial bet of five dollars then, statistically speaking, he will break even in the long run. This can be proven theoretically as follows:
$10.83 x 24/52= $5
 |  |
 |
 |
Conclusion-
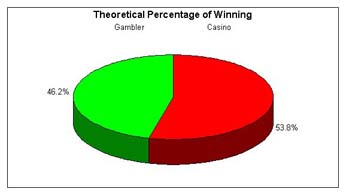
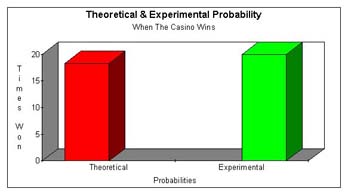
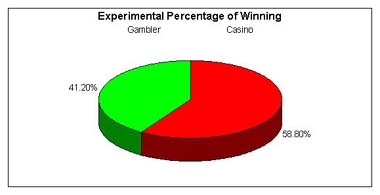
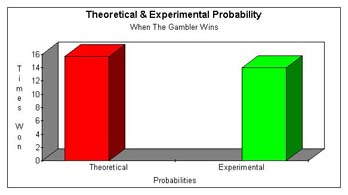
After playing 34 times the gambler won 14 times and the dealer won 20 times. That means the experimental probability for the gambler winning is 14/34 and the experimental probability for the dealer winning is 20/34. The probability for the gambler winning is slighty lower than the theoretical probability which is 15.692/34. You find this by multiplying 24/52 x 34. Also, the experimental probability of the casino winning is slightly higher than the theoretical probability which is 18.3/34. You find this by multiplying 28/52 x 34. The theoretical probability is found by using the formula:
number of favorable outcomes x (n/34)
number of possible outcomes
The differences in the in experimental probability and theoretical probability could have been caused by errors such as not shuffling properly or not playing the game enough times. The casino always makes money on Over-Under because both the theoretical and experimental probabilities show that it will. The theoretical probability of winning is 6/13 giving it 7:8 odds in favor of winning. The experimental probability showed that the casino wins 10/17 giving the casino 10:7 odds in favor of winning. |
 |
 |
| Back to: | [Project Description] | [Student Work Homepage] | [Professional Stuff] |